5.5.1 $d/d\theta\sin(\theta)$
$$\frac{d}{d\theta}\sin(\theta)=\cos(\theta)$$
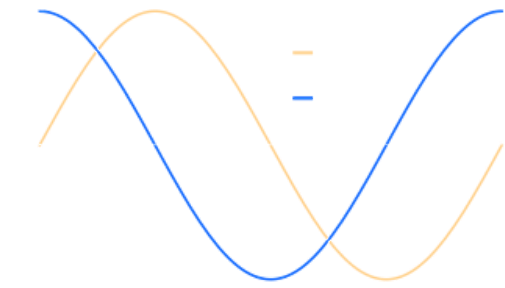
Proof
Insert $\sin(\theta)$ into the
derivative function
$$\lim_{\Delta\theta→0}\frac{\sin(\theta+\Delta\theta)-sin(\theta)}{\Delta\theta}$$
Expand the
sine addition
$$\lim_{\Delta\theta→0}\frac{\sin(\Delta\theta)·\cos(\theta)+\sin(\theta)·\cos(\Delta\theta)-sin(\theta)}{\Delta\theta}$$
Factor into terms of
limits of trig functions
$$\lim_{\Delta\theta→0}\bigg(\frac{\sin(\Delta\theta)}{\Delta\theta}·\cos(\theta)+\frac{\cos(\Delta\theta)-1}{\Delta\theta}·\sin(\theta)\bigg)$$
Solve the limits
$$1·\cos(\theta)+0·\sin(\theta)$$
Simplify
5.5.2 $d/d\theta\cos(\theta)$
$$\frac{d}{d\theta}\cos(\theta)=-\sin(\theta)$$
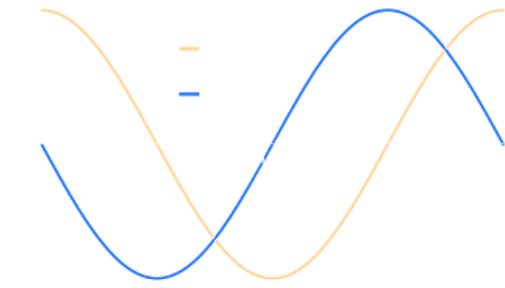
Proof
Insert $\cos(\theta)$ into the
derivative function
$$\lim_{\Delta\theta→0}\frac{\cos(\theta+\Delta\theta)-cos(\theta)}{\Delta\theta}$$
Expand the
cosine addition
$$\lim_{\Delta\theta→0}\frac{\cos(\Delta\theta)·\cos(\theta)-\sin(\theta)·\sin(\Delta\theta)-cos(\theta)}{\Delta\theta}$$
Factor into terms of
limits of trig functions
$$\lim_{\Delta \theta→0}\bigg(\frac{\cos(\Delta\theta)-1}{\Delta\theta}·\cos(\theta)-\frac{\sin(\Delta\theta)}{\Delta\theta}·\sin(\theta)\bigg)$$
Solve the limits
$$0·\cos(\theta)-1·\sin(\theta)$$
Simplify
5.5.3 $d/d\theta\tan(\theta)$
$$\frac{d}{d\theta}\tan(\theta)=\sec^2(\theta)$$
Proof
Write in terms of the
tangent cofunctions
$$\frac{d}{d\theta}\frac{\sin(\theta)}{\cos(\theta)}$$
Apply the
quotient rule
$$\frac{d}{d\theta}\frac{\cos(\theta)·\sin(\theta)'-\sin(\theta)·\cos(\theta)'}{\cos^2(\theta)}$$
Derive
$$\frac{\cos^2(\theta)+\sin^2(\theta)}{\cos^2(\theta)}$$
Substitute the
right angle identity
$$1/\cos^2(\theta)$$
Write in terms of its cofunction
5.5.4 $d/d\theta\cot(\theta)$
$$\frac{d}{d\theta}\cot(\theta)=-\csc^2(\theta)$$
Proof
Write in terms of the
cotangent cofunctions
$$\frac{d}{d\theta}\frac{\cos(\theta)}{\sin(\theta)}$$
Apply the
quotient rule
$$\frac{d}{d\theta}\frac{\sin(\theta)·\cos(\theta)'-\cos(\theta)·\sin(\theta)'}{\sin^2(\theta)}$$
Derive
$$-\frac{\sin^2(\theta)+\cos^2(\theta)}{\sin^2(\theta)}$$
Substitute the
right angle identity
$$-1/\sin^2(\theta)$$
Write in terms of its cofunction
5.5.5 $d/d\theta\sec(\theta)$ 🔧
$$\frac{d}{d\theta}\sec(\theta)=\sec(\theta)·\tan(\theta),\medspace\cos(\theta)\ne 0$$
Proof
5.5.6 $d/d\theta\csc(\theta)$ 🔧
$$\frac{d}{d\theta}\csc(\theta)=-\csc(\theta)·\cot(\theta),\medspace\sin(\theta)\ne 0$$
Proof
5.5.7 $d/dx \sin^{-1}(x)$ 🔧
$$\frac{d}{dx}\sin^{-1}\bigg(\pm\frac{x}{a}\bigg)=\pm\frac{1}{\sqrt{a^2-x^2}},\medspace |x| \lt 1$$
Proof
5.5.8 $d/dx \cos^{-1}(x)$ 🔧
$$\frac{d}{dx}\cos^{-1}\bigg(\pm\frac{x}{a}\bigg)=\mp\frac{1}{\sqrt{a^2-x^2}},\medspace |x| \lt 1$$
Proof
5.5.9 $d/dx \tan^{-1}(x)$ 🔧
$$\frac{d}{dx}\tan^{-1}\bigg(\pm\frac{x}{a}\bigg)=\pm\frac{a}{x^2+a^2}$$
Proof
5.5.A $d/dx \cot^{-1}(x)$ 🔧
$$\frac{d}{dx}\cot^{-1}\bigg(\pm\frac{x}{a}\bigg)=\mp\frac{a}{x^2+a^2}$$
Proof
5.5.B $d/dx \sec^{-1}(x)$ 🔧
$$\frac{d}{dx}\sec^{-1}\bigg(\pm\frac{x}{a}\bigg)=\pm\frac{a}{\sqrt{x^2·(x^2-a^2)}},\medspace |x| \gt 1$$
Proof
5.5.C $d/dx \csc^{-1}(x)$ 🔧
$$\frac{d}{dx}\csc^{-1}\bigg(\pm\frac{x}{a}\bigg)=\mp\frac{a}{\sqrt{x^2·(x^2-a^2)}},\medspace |x| \gt 1$$
Proof