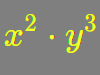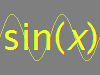2.1.1 Universal Properties
Exponentiation is repeated multiplication. An exponent is the number of times to "times" a number.
- Exponents do not commute: $x^a≠a^x$
- Exponents do not associate: $x^{(a^b)}≠{(x^a)}^b$
- Factoring is the condensing of terms: $x^3$
- The reverse of factoring is expansion: $x·x·x$
2.1.2 Negative Exponents
$$x^{-a}=\frac{1}{x^a}$$
Deductive Logic
Multiplication is reversible with division, therefore exponential reduction yields inverses once reaching negatives.
| $$x^3=1·x·x·x$$ |
$$3^3=27$$ |
| $$x^2=1·x·x$$ |
$$3^2=9$$ |
| $$x=1·x$$ |
$$3^1=3$$ |
| $$x^0=1$$ |
$$3^0=1$$ |
| $$x^{-1}=1/x$$ |
$$3^{-1}=1/3$$ |
| $$x^{-2}=1/(x·x)$$ |
$$3^{-2}=1/9$$ |
| $$x^{-3}=1/(x·x·x)$$ |
$$3^{-3}=1/27$$ |
2.1.3 Power Rule
$$x^a·x^{\pm b}=x^{a \pm b}$$
Deductive Logic
$x$ is multiplied $a$ times and $x$ is multiplied $b$ times, and if the terms are multiplied to each other, this is a partially
expanded form
Example
$$2^3·2^4=8·16=128=2^7$$
$$2^3·2^4=2^{3+4}=2^7=128$$
2.1.4 Higher Exponentials
Evaluate starting from the highest exponent first, working downward, minding parenthesized terms along the way.
$$x^{a^{b^{c^d}}}=x^{\Big(a^{\big(b^{(c^d)}\big)}\Big)}$$
Tetration
A unique case of one value in repeated exponentiation, often represented as
$$x^{x^{x^{x^x}}}=\phantom{}^5x$$
2.1.5 Power Distribution
$${(x^a·y^{\pm b})}^c=x^{a·c}·y^{\pm b·c}$$
Deductive Logic
Distribute the exponential $c$ by expanding into ${(x^a)}^c·{(y^{±b})}^c$. The terms are multiplied $c$ times
Example 1
$$(2^3)^2=2^{(3·2)}$$
$$8^2=2^6=64$$
Example 2
Given $3·x–5·y=2$, evaluate $8^x/32^y$
$$\frac{8^x}{32^y}=\frac{{(2^3)}^x}{{(2^5)}^y}=\frac{2^{3·x}}{2^{5·y}}$$
Apply the
power rule, then substitute $3·x–5·y$ for $2$
$$\frac{2^{3·x}}{2^{5·y}}=2^{3·x-5·y}=2^2$$
2.1.6 Roots
Reciprocal exponents represent roots and are
multiplicative inverses of their integer counterparts.
$$x^{1/n}=\sqrt[n]{x}$$
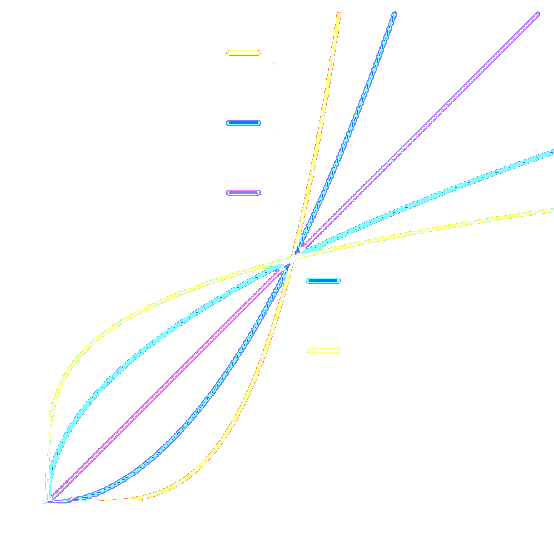
2.1.7 Rational Exponents
$$x^{p/q}={(\sqrt[q]{x})}^p=\sqrt[q]{x^p},\medspace\forall x≥0$$
2.1.8 Root Expansion & Factoring
$$\sqrt[n]{x·y^{\pm 1}}=\sqrt[n]{x}·\sqrt[n]{y^{\pm 1}},\medspace x>0 \land y>0$$
Rule
Even though $1^2=1$ and $(-1)^2=1$, radicands cannot be factored into two negatives because it creates the following logical fallacy
$\qquad 2=2$
$\qquad 2=1+1$
$\qquad 2=1+\sqrt{1}$
$\qquad 2=1+\sqrt{-1·-1}$
$\qquad 2=1+\sqrt{-1}·\sqrt{-1}$
$\qquad 2=1+(\sqrt{-1})^2$
$\qquad 2=1-1$
$\qquad 2=0$
$\qquad $
No solution
2.1.9 Even Roots of Even Powers
$$\sqrt[n]{x^n}=|x|,\medspace\{ 2·n | n \isin \Z \}$$
2.1.A Scientific Notation
All numbers are multiples of ten to a power in accordance with the leading digit
$$299792458=2.99792458·10^8$$
$$0.0820574=8.20574·10^{-2}$$