Deipnosophism

Who made you god of geometry?
December 2024

Why are parallel lines considered degenerate conics and hyperboloids considered standard quadrics? Lets follow some facts here, and highlight the ones that are inconsistent (pink). My only question is - Why are they inconsistent?

2D Conic Sections	3D Quadric Surfaces
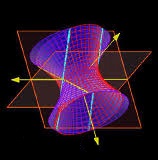
Parallel lines (cyan) can be rotated to form a hyperboloid of one sheet.	Hyperboloids of one sheet can be rotated to form a hyper-hyperboloid (which unimaginatively is normally also just called a hyperboloid).

Parallel lines is the only conic section which does not occur with any planar intersection on the double cone.	Hyperboloids of one sheet do not occur with any field intersection on the double hypercone.
Parallel lines are considered degenerate.	Hyperboloids of one sheet are considered standard.
A hyperboloid of one sheet can be intersected to produce circles, ellipses, hyperbolas, parallel lines, and intersecting lines.	A hyper-hyperboloid of one sheet can be intersected to produce spheres, ellipsoids, hyperboloids, cylinders, and the double cone.
Intersecting lines are a specific case only of a double cone, a plane intersecting at its apex, and a hyperboloid of one sheet, a plane intersecting at its transverse axis.	The double cone is a specific case only of a double hypercone, a field intersecting at its apex, and a hyper-hyperboloid of one sheet, a field intersecting at its transverse axis.
When the transverse axis of a hyperboloid of one sheet approaches its asymptotes, it forms a double cone.	When the transverse axis of a hyper-hyperboloid of one sheet approaches its asymptotes, it forms a double hypercone.

A parabola and a point are specific cases of the cone, the parabola intersecting through it on any plane parallel to a single line on its surface, having only an eccentricity of 1 and not appearing on the hyperboloid of one sheet.	A paraboloid and a point are specific cases of the hypercone, the paraboloid intersecting through it on any field parallel to a single line on its surface, having only an eccentricity of 1, and not appearing on the hyper-hyperboloid of one sheet.
Hyperbolas "of two sheets" are standard conics, but "hyperbolas of one sheet" are never mentioned. They can both be graphed with the same exact equation and viewed this way: "One sheet" cyan "Two sheets" yellow	Hyperboloids of one sheet and of two sheets are standard quadrics. They can only be represented with opposite signs for the variable side of the same exact equation. Ironically, graphing both in the same field with only the sign reversal on the variable side and splitting it down the middle of both symmetrically produces the exact same image below.

Conclusion: We should reevaluate conics/quadrics to include the hyperboloid/hyper-hyperboloid of one sheet as supersets wherein the double cone/hypercone are special cases, and since the 5D hyperboloid of one sheet encapsulates them all, simply call them hyperbolics.

We should also drop the notion that something isn't beautiful ("degenerate") without all the right curves, because it is effectively meaningless when viewing the whole.

Return to top

Honey, I Shrunk the ~~Kids~~ Universe
October 2024

What if the universe really is infinitesimal? Think of how much this would suggest. Everything in the universe would literally still be one thing, cosmos, all connected. From outside of the universe, it would appear as a particle. So then are particles within our universe other universes, and are there infinitely more universes on the same level as ours all within a much larger universe? So then, could there be infinitely tiered universes where each is just one of countless particles in another? Furthermore, if the universe is infinitesimal then how do we appear separate from everything else? Then again, how does everything in it follow the same physics as if connected?

Our universe is expanding. Expanding into what? Spacetime is a thing, an object, and true void is impossible. Is it possible that in our infinitesimal universe that something would be causing the perception of the expansion? Could it be possible that the expansion we observe is the result of something overall, like loss of energy? That would even explain the rates of change in expansion throughout its phases, as if the universe were a particle interacting with other particles in those points of time. We would have to assume the rate of energy loss is the same as everywhere else since we are made of the same particles as everywhere else, and have not observed deviations to oppose the notion.

Insignificance never had such a greater meaning.

Return to top

You put what in my chemicals?
July 2024

What if a different type of atomic nucleus existed? Aside from particles governed by the strong force, that electrons could form orbitals around? The orbital patterns would probably be different as well, producing a whole new type of atom right alongside of those in the periodic table. Could they coexist with our familiar atoms and lead to hybrid compounds? We can use this concept as rubber science to explain made up chemical elements often named in sci-fi series, especially in Star Trek.

When we speculate that atoms can comprise of both strong force particles and said hypothetical particles, chances are they would warp electron orbitals even further. We can then chart out a two-dimensional table of chemical elements with linear progression for the intervals of each set. So in this case, let's then assume there are 118 hypothetical elements by themselves (if ever proven possible, it probably won't be exact). That's 118 hypothetical elements plus 118 strong force nuclei elements plus 118² possible combinations. With hybridizing the types of nuclei, it totals 14160 possible chemical elements.

You can forget naming them at this point.

Return to top